We will use example provided in the official implementation of the KAN paper. Install the library with
pip install pykan
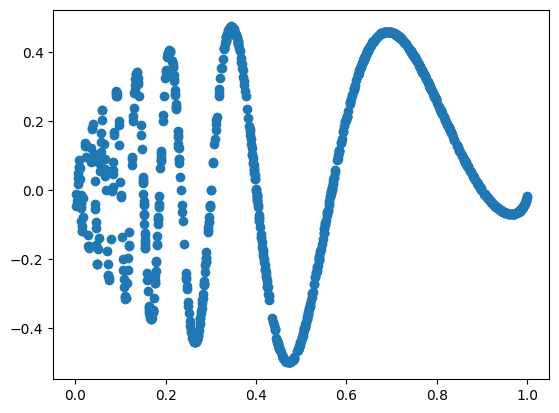
Function Fitting We will take some interesting test functions from Wavelet Regression notebook.
The Doppler function is \[
f(x) = \sqrt{x(1-x)} \sin(\frac{2.1\pi}{x+0.05}) \\
x \sim U[0,1]
\]
import torch
import matplotlib.pyplot as plt
import numpy as np
from kan.utils import create_dataset
torch.set_default_dtype(torch.float64)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print('device is: ',device)
f = lambda x: torch.sqrt(x[:,[0]]*(1-x[:,[0]]))*torch.sin((2*np.pi)/(x[:,[0]]+.1))
dataset = create_dataset(f, n_var=1, device=device, ranges=[0,1])
print('train input data shape', dataset['train_input'].shape)
print('train label data shape', dataset['train_label'].shape)
plt.scatter(dataset['train_input'],dataset['train_label'])
device is: cpu
train input data shape torch.Size([1000, 1])
train label data shape torch.Size([1000, 1])
# create a KAN: 1D inputs, 1D output, and 5 hidden neurons. cubic spline (k=3), 5 grid intervals (grid=5).
from kan import KAN
model = KAN(width=[1,3,1], grid=5, k=3, seed=0, device=device)
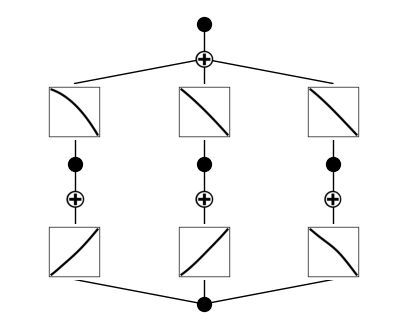
# plot KAN at initialization
model(dataset['train_input'])
model.plot()
# train the model
model.fit(dataset, opt="LBFGS", steps=50, lamb=0.001);
checkpoint directory created: ./model
saving model version 0.0
| train_loss: 8.76e-02 | test_loss: 9.21e-02 | reg: 7.97e+00 | : 100%|█| 50/50 [00:09<00:00, 5.53it
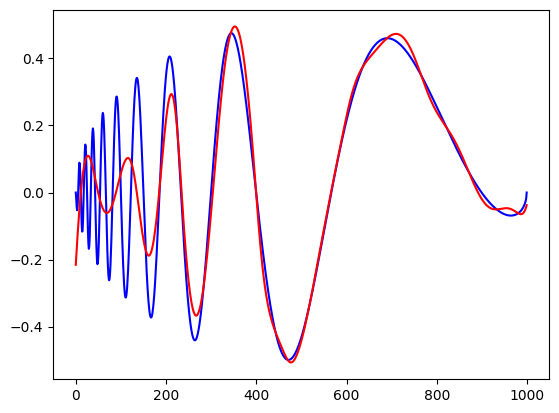
# let us look at the recontruction
X = dataset['train_input']
n = 1000
X[:,0] = torch.linspace(0,1,steps=n)
y = f(X)
y = y[:,0].detach().numpy()
yh = model.forward(X)
yh = yh[:,0].detach().numpy()
plt.plot(y,color='blue')
plt.plot(yh, color='red')
plt.show()
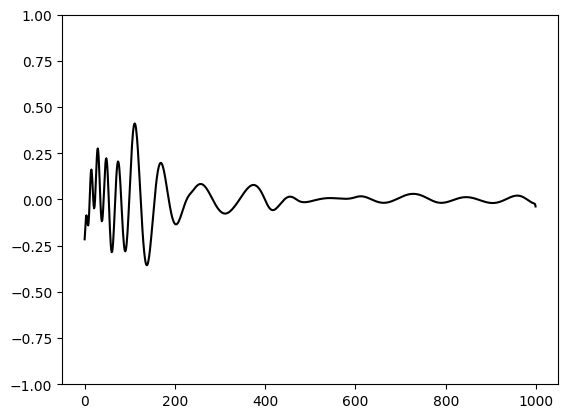
plt.plot(yh-y, color='black')
plt.ylim(-1,1)
plt.show()